Hull Speed Calculator

What is Hull Speed?

Hull speed is the theoretical maximum speed at which a displacement hull can travel efficiently through the water. First described by naval architect William Froude in the 19th century, this fundamental concept in naval architecture explains why traditional sailboats and displacement powerboats face a practical speed limit, regardless of how much power you add.

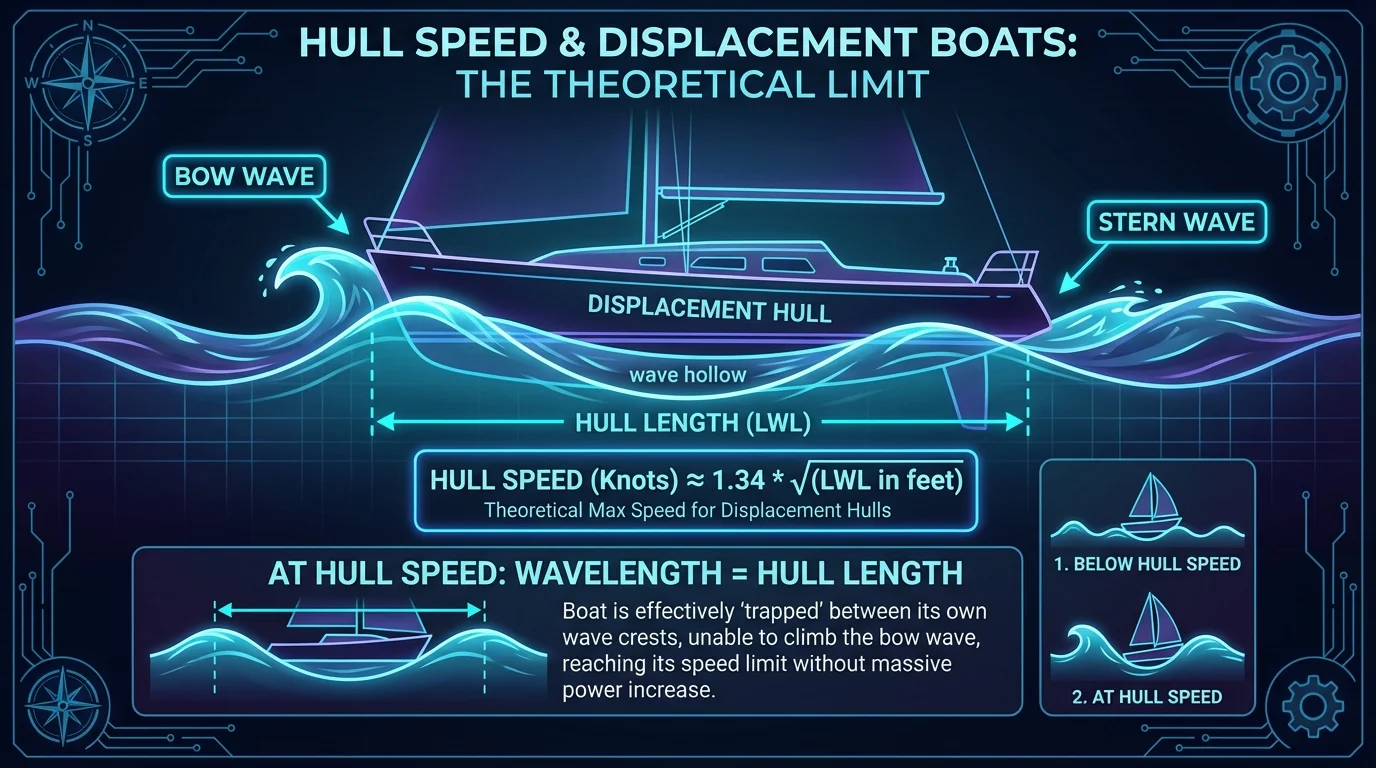
As a displacement vessel moves through water, it creates waves. The faster the boat moves, the longer these waves become. At hull speed, the boat's waterline length equals the wavelength of its bow wave, and the boat essentially becomes trapped between its own bow and stern waves. Beyond this point, wave-making resistance increases exponentially, requiring massive amounts of additional power for minimal speed gains.

The Hull Speed Formula

The classic hull speed formula is remarkably simple:

How to Calculate Hull Speed

Hull speed is calculated using a constant factor multiplied by the square root of the waterline length. The standard factor for displacement hulls is 1.34.

The Physics of Hull Speed

Understanding hull speed requires understanding wave mechanics. When a boat moves through water, it displaces water and creates waves. The speed at which these waves travel is determined by their wavelength according to the deep water wave speed formula:

Wave Speed = 1.34 × √(Wavelength) (in nautical terms)

At hull speed, the boat's waterline length matches the wavelength of its bow wave. The boat is effectively trying to climb its own bow wave while simultaneously being pulled down by the stern wave trough. This creates a phenomenon where:

• Below Hull Speed: The boat sits relatively level, with wave resistance increasing linearly with speed.
• At Hull Speed: The boat begins to squat stern-down as it tries to climb between its own bow and stern waves.
• Beyond Hull Speed: Resistance increases exponentially. Doubling the power might only increase speed by 10-20%.

When Boats Can Exceed Hull Speed

While hull speed represents a critical threshold for displacement vessels, several types of boats routinely exceed it:

Planing Hulls

Powerboats with planing hulls are specifically designed to rise up and skim across the water surface at high speeds. Once "on plane," they're no longer displacement vessels and aren't constrained by hull speed. Most recreational powerboats, jet skis, and racing boats use planing hulls.

Semi-Displacement Hulls

These hybrid designs combine characteristics of displacement and planing hulls. They can exceed hull speed more efficiently than pure displacement hulls but don't fully plane. Many modern trawlers and motor yachts use semi-displacement designs.

Multihulls

Catamarans and trimarans have narrow hulls with very high length-to-beam ratios, which reduces wave-making resistance. Combined with their low wetted surface area, multihulls can regularly exceed displacement hull speed calculations, especially when sailing.

Surfing and Displacement Sailing

Even traditional displacement sailboats can exceed hull speed when surfing down waves. The wave provides the energy to overcome resistance, allowing speeds of 1.5 to 2 times theoretical hull speed for brief periods.

Speed-to-Length Ratio (S/L Ratio)

The Speed-to-Length Ratio provides a dimensionless number that allows comparison between vessels of different sizes. It's calculated as:

S/L Ratio Benchmarks

• Below 1.0: Efficient displacement cruising. Low fuel consumption, comfortable motion.
• 1.0-1.2: Fast displacement cruising. Still relatively efficient.
• 1.34: Theoretical hull speed. Resistance begins to increase dramatically.
• 1.5-2.0: Above hull speed for displacement vessels. Semi-displacement or surfing conditions.
• Above 2.5: Planing or high-performance vessel behavior.

Historical Context

The concept of hull speed emerged from the work of William Froude (1810-1879), an English engineer and naval architect who pioneered the scientific study of ship resistance. In the 1860s and 1870s, Froude conducted extensive towing tank experiments and developed the dimensionless "Froude Number," which relates a vessel's speed to wave-making resistance.

His research revealed that geometrically similar vessels experience the same wave resistance patterns at the same Froude Number, regardless of absolute size. This discovery revolutionized ship design and remains fundamental to naval architecture today. The hull speed formula we use is a simplified practical application of Froude's more complex theoretical work.

Practical Applications

Understanding hull speed helps sailors and boaters in several ways:

• Realistic Expectations: Know your boat's practical maximum speed without adding excess power.
• Efficient Cruising: Operate at 80-90% of hull speed for optimal fuel efficiency and range.
• Boat Selection: Compare different vessels using S/L ratios to understand performance characteristics.
• Power Requirements: Avoid over-powering a displacement hull, which provides little benefit beyond hull speed.
• Passage Planning: Calculate realistic arrival times based on achievable speeds.

Limitations of Hull Speed Theory

While hull speed is a useful guideline, it's not an absolute law. Modern hull designs, lightweight materials, and advanced hydrodynamics have pushed the boundaries of what's possible:

• Ultra-light displacement boats (ULDB) can exceed traditional hull speed calculations
• Fine-entry bows and efficient hull shapes reduce wave-making resistance
• Active trim systems and hydrofoils can modify effective waterline length
• The formula assumes deep water; shallow water significantly alters resistance patterns

Think of hull speed as a threshold rather than a barrier—a point where efficiency drops dramatically, but not an impenetrable limit.