The Martingale is the most famous betting system in gambling history—and the most dangerous. It promises guaranteed profits through a simple rule: double your bet after every loss. When you eventually win, you’ll recover all losses plus one unit of profit. Mathematically elegant. Practically devastating. Here’s exactly how it works, why it appears to work, and why it will ultimately destroy your bankroll.

Key Highlights
- The core rule: Double your bet after every loss, return to base bet after every win
- The promise: Every winning spin recovers all previous losses plus one unit profit
- The reality: Table limits and finite bankrolls make catastrophic loss inevitable
- After 10 losses: A $10 starting bet becomes $10,240—just to win $10
- The math: Expected value remains negative; house edge is preserved regardless of bet sizing
- Short-term success rate: ~80% in one hour, but drops to ~37% over eight hours
How the Martingale Works
The Martingale system originated in 18th-century France and applies to any even-money bet: red/black in roulette, pass/don’t pass in craps, or player/banker in baccarat. The rules are simple:
- Start with a base bet (e.g., $10 on red)
- If you win, collect your winnings and bet the base amount again
- If you lose, double your bet (now $20 on red)
- Continue doubling after each loss until you win
- When you win, you’ve recovered all losses plus your original base bet as profit
- Return to step 1
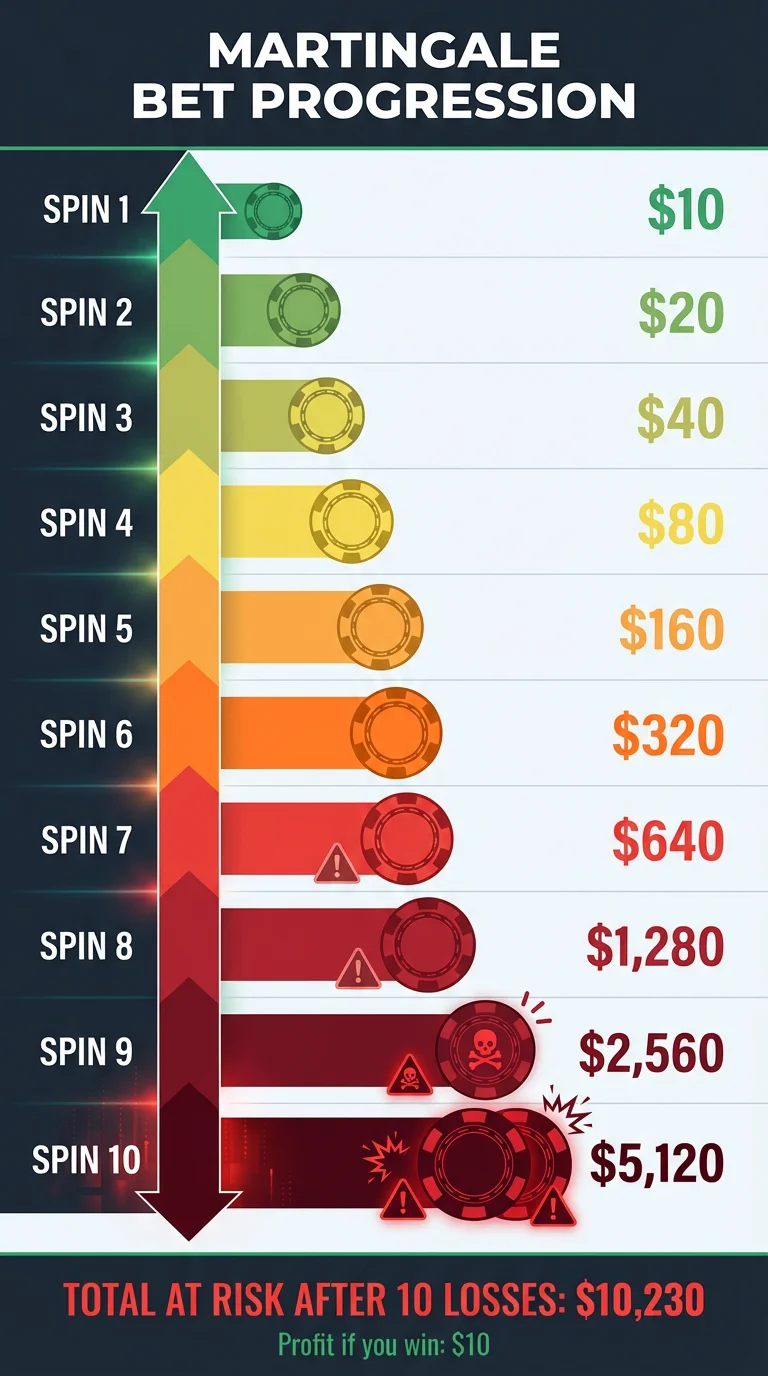
A Worked Example
Let’s trace through a losing streak with a $10 base bet:
| Spin | Bet | Result | Cumulative Loss | Next Bet |
|---|---|---|---|---|
| 1 | $10 | Loss | $10 | $20 |
| 2 | $20 | Loss | $30 | $40 |
| 3 | $40 | Loss | $70 | $80 |
| 4 | $80 | Loss | $150 | $160 |
| 5 | $160 | Loss | $310 | $320 |
| 6 | $320 | Loss | $630 | $640 |
| 7 | $640 | WIN | — | +$10 profit |
After seven spins—six losses and one win—you’ve wagered a total of $1,270 and walked away with $10 profit. The system “worked.” But notice the asymmetry: you risked $1,270 to win $10. And if spin 7 had also lost, you’d need to bet $1,280 next—total exposure of $2,550—still just to win $10.
Why It Appears to Work
The Martingale’s seductive appeal comes from its high short-term win rate. In European roulette, the probability of losing six consecutive even-money bets is approximately 1.8% (on any given sequence of six spins). That means 98.2% of the time, you’ll win within six spins and pocket your base bet profit.
Research shows that Martingale players have roughly an 80% chance of finishing ahead after one hour of play, compared to only 46% for flat-betting players. The strategy genuinely does produce more winning sessions in the short term.
The Illusion: You win frequently and lose rarely. This creates the powerful psychological impression of a “working system”—but the rare losses are catastrophic enough to wipe out all previous wins and more.
Why It Inevitably Fails
The Martingale fails for multiple interconnected reasons, all stemming from a fundamental mathematical reality: no betting system can overcome a negative expected value game.
1. Exponential Bet Growth
Doubling creates exponential growth that quickly reaches absurd levels:
| Consecutive Losses | Next Bet Required | Total Wagered | Potential Profit |
|---|---|---|---|
| 5 | $320 | $630 | $10 |
| 7 | $1,280 | $2,550 | $10 |
| 10 | $10,240 | $20,470 | $10 |
| 15 | $327,680 | $655,350 | $10 |
After just 10 losses, you need over $10,000 on the table—to win $10. The risk-to-reward ratio becomes increasingly absurd with each losing spin.
2. Table Limits Stop the Strategy
Casinos implement maximum bet limits precisely because they understand the Martingale. A typical roulette table might have a $10 minimum and $500 maximum. With a $10 base bet, you can only double six times before hitting the ceiling:
$10 → $20 → $40 → $80 → $160 → $320 → $640 (exceeds limit)
On the seventh loss, you cannot place the required $640 bet. The system collapses. You’ve lost $630 with no way to recover.
3. Finite Bankrolls
Even without table limits, your personal bankroll creates the same constraint. If you have $1,000 to gamble with and start with $10 bets, you can sustain six consecutive losses ($630 total). A seventh loss ($640 bet) exceeds your remaining funds.
The Martingale only “works” with infinite wealth. No one has infinite wealth.
4. Losing Streaks Are More Common Than You Think
Here’s the critical insight most Martingale believers miss: while the chance of losing six consecutive bets in any specific six-spin sequence is only 1.8%, the probability of experiencing a six-bet losing streak at some point during extended play is dramatically higher.
- Over 200 spins: ~84% chance of a 6+ losing streak
- Over 200 spins: ~11% chance of a 10+ losing streak
- The probability of 10 consecutive losses on a single-zero wheel: 1 in 784
Play long enough, and the devastating streak will come.
5. The House Edge Is Preserved
This is the mathematical death blow. The house edge on European roulette even-money bets is 2.70%. No betting pattern changes this. The Martingale redistributes when you experience wins and losses, but it doesn’t change the expected value of each bet.
A mathematical analysis shows that the normalized expected result for a Martingale player is exactly -2.70%—identical to flat betting. The strategy changes your variance (more small wins, fewer but larger losses) without touching the house edge.
The Mathematical Truth:
“Despite the fact that the gambler usually wins a small net reward, thus appearing to have a sound strategy, the gambler’s expected value remains negative because the small probability of a catastrophic loss exactly balances with the expected gain.”
— Wikipedia, Martingale (betting system)
The Optional Stopping Theorem
For the mathematically inclined, the impossibility of the Martingale is formally proven by the optional stopping theorem from probability theory. In plain terms: if you’re playing a negative expected value game, no stopping rule or betting pattern can produce positive expected value.
The theorem requires either infinite wealth, no table limits, or infinite time—conditions that don’t exist in reality. Under real-world constraints, expected losses remain negative.
Short-Term vs. Long-Term Results
The Martingale creates a specific tradeoff between session win rate and eventual ruin:
| Session Length | Martingale Win Rate | Flat Betting Win Rate |
|---|---|---|
| 1 hour | ~80% | ~46% |
| 4 hours | ~55% | ~45% |
| 8 hours | ~37% | ~44% |
| Long-term (infinite) | 0% (certain ruin) | 0% (certain loss) |
The Martingale front-loads your wins and back-loads your losses. It’s not magic—it’s redistribution. The longer you play, the more likely you are to hit the catastrophic losing streak that wipes out all previous gains.
The Gambler’s Fallacy Connection
Martingale believers often fall prey to the gambler’s fallacy: the belief that after multiple losses, a win becomes “due.” If red hasn’t hit in six spins, surely it must be more likely now?
It isn’t. Each spin is independent. The wheel has no memory. The probability of red on spin 7 is exactly the same as on spin 1—approximately 48.6% on a European wheel. Previous results provide zero information about future outcomes.
The Martingale doesn’t work because of probability catching up—it “works” until your bankroll or the table limit runs out first.
Why Casinos Welcome Martingale Players
Casinos don’t ban Martingale betting. They don’t need to. The math is entirely in their favor. A Martingale player loses the same expected amount as a flat bettor—they just lose it in a more dramatic fashion.
Casino operators understand that Martingale players will eventually hit a losing streak that exceeds their bankroll or the table limit. When that happens, they don’t just lose their current session—they lose all the “profits” from previous sessions too.
The table limit exists specifically to ensure this happens. It’s not a coincidence that most tables have a spread of about 50-100x between minimum and maximum bets—enough to allow 6-7 doubles before hitting the cap.
Variations That Don’t Help
Several Martingale variants exist, all sharing the same fundamental flaw:
- Grand Martingale: Double plus one unit after each loss. Increases profit per win but accelerates bankroll depletion.
- Mini Martingale: Cap the progression at a certain level (e.g., 4 doubles max). Reduces catastrophic loss size but doesn’t eliminate negative expected value.
- Anti-Martingale (Paroli): Double after wins instead of losses. Different variance profile, same house edge.
No betting system overcomes negative expected value. Period.
The Bottom Line
The Martingale is mathematically elegant and practically ruinous. It produces frequent small wins that create the illusion of a working system while guaranteeing eventual catastrophic loss. The house edge remains exactly the same as flat betting—you just experience it differently.
If you choose to use the Martingale, do so with clear eyes: you’re trading many small wins for occasional total bankroll wipeouts. You might win in the short term—but the longer you play, the more certain your ruin becomes. Casinos have table limits specifically because they understand this math. Maybe you should too.
FAQs
In the short term, yes—you’ll win frequently. Over time, no. The strategy produces an 80% win rate in one-hour sessions but drops to 37% over eight hours. Eventually, a losing streak will exceed your bankroll or hit the table limit. The house edge remains unchanged at 2.70% (European) or 5.26% (American).
Because it doesn’t change the house edge. Martingale players lose the same expected amount as flat bettors—just in larger, less frequent chunks. Table limits ensure that eventual losing streaks will exceed players’ ability to continue doubling, resulting in catastrophic losses that wipe out all previous wins.
To survive 10 consecutive losses with a $10 base bet, you need $20,470. To survive 15 losses, you need $655,350. Even then, the 16th loss would require $327,680. The strategy requires exponentially increasing bankrolls while profit remains fixed at just one base unit.
On a European wheel betting red/black, the probability of losing 10 consecutive spins is approximately 1 in 784 (0.13%). However, over 200 spins of play, there’s roughly an 11% chance of experiencing such a streak. Extended play makes long losing streaks nearly inevitable.
No. The house edge (2.70% European, 5.26% American) applies to every bet regardless of betting pattern. Mathematical proofs like the optional stopping theorem confirm that no betting system can produce positive expected value in a negative-expectation game. Bet sizing only changes variance, not edge.
Martingale doubles after losses to recover; Anti-Martingale (Paroli) doubles after wins to capitalize on streaks. Both have identical expected value (negative, matching the house edge). They simply produce different variance patterns—Martingale has frequent small wins and rare large losses; Anti-Martingale has frequent small losses and rare large wins.
A larger base bet just accelerates everything—faster profit accumulation but faster approach to table limits and bankroll exhaustion. A $100 base bet hits the table limit ($500 max example) after just two losses. The fundamental math remains unchanged: house edge preserved, eventual ruin certain.
European roulette is always better due to its lower house edge (2.70% vs 5.26%), but the Martingale fails on both. On American roulette, losing streaks are more likely because the extra double zero reduces your win probability from 48.6% to 47.4%. Use European wheels if available, but expect eventual losses either way.